W przygotowaniu

nr 5-6(25-26) 2017
dostępny
po 29.12.2017

Wydanie aktualne

nr 3-4(23-24) 2017
dostępny w pdf, wydanie flash tutaj

Wydania archiwalne

nr 1-2(21-22) 2017
dostępny w pdf, wydanie flash tutaj

nr 1-2(19-20) 2015
dostępny w pdf, wydanie flash tutaj

numer 1(18) 2014
dostępny w pdf, wydanie flash tutaj

numer 1(17) 2013
dostępny w pdf, wydanie flash tutaj

numer 1(16) 2012
dostępny
w archiwum

numer 1(15) 2011
dostępny
w archiwum

numer 4(14) 2010
HD dostępny
w archiwum

numer 3(13) 2010
HD dostępny
w archiwum

numer 2(12) 2010
dostępny
w archiwum

numer 1(11) 2010 dostępny
w archiwum

Obserwuj @CADblog_pl

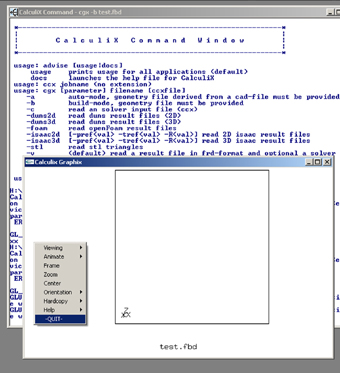
Fragment artykułu z nr 2(3) maj 2009 (kompletne wydanie do pobrania z Archiwum)

Gra w kolory, czyli... oprogramowanie do analiz i symulacji: CalculiX cz. I

Projektowanie wspomagane komputerowo znacznie wykroczyło poza obszary, które jeszcze do niedawna były domeną desek kreślarskich, a także logarytmicznych suwaków i kalkulatorów. Obliczenia wytrzymałościowe, analizy zmęczeniowe, obliczenia wartości wielkości przepływów cieczy, ich wpływu na wielkość i rozkład drgań i naprężeń w układzie konstrukcji itp. stanowią jedną z dynamiczniej rozwijających się dziedzin z pogranicza matematyki, informatyki i inżynierii. Korzystanie w celu przeprowadzenia analiz i obliczeń z wyspecjalizowanego oprogramowania przestało być koniecznością, gdyż liczący się producenci coraz częściej implementują tego typu funkcjonalności bezpośrednio do swoich systemów; często dzieje się tak na drodze akwizycji. Gdy jednak nie dysponujemy takim środowiskiem programowym, a nasze finanse okazują się ograniczone, możemy sięgnąć po wysokiej klasy wyspecjalizowane narzędzie, dostępne bezpłatnie, rozwijane przez wiele podmiotów. Jest nim właśnie CalculiX...

OPRACOWANIE: Maciej Stanisławski

Komputerowe systemy do wykonywania analiz i symulacji z wykorzystaniem metody elementów skończonych (MES – ale uwaga, ang. skrót MES oznacza Mechanical Events Simulation; patrz ramka) zrewolucjonizowały pracę inżynierów. Zredukowały czas potrzebny na wykonywanie skomplikowanych działań na układach równań, macierzach itp., w zamian pozwalając na wykonywanie wspomnianych analiz w środowisku będącym swoistym standardem współczesnych systemów CAE. Wspomniany program jest właśnie tego typu systemem, narzędziem – jak kto woli. Ale zanim przejdziemy do jego omówienia, kilka słów teorii...

MES w oprogramowaniu dla inżynierów projektantów
Metoda elementów skończonych stała się powszechnie stosowanym narzędziem obliczeń inżynierskich. Łatwo zauważyć, iż rozwój metody elementów skończonych przebiega równolegle z rozwojem techniki komputerowej. Pierwsze prace wskazujące na praktyczne zastosowania MES opublikowane zostały w latach czterdziestych ubiegłego wieku. W tych samych latach zresztą powstały pierwsze komputery. Początkowo obliczenia przeprowadzane za pomocą metody elementów skończonych dotyczyły obiektów o bardzo prostych geometriach (najczęściej modelowanych jako jednowymiarowe) i stałych własnościach materiałowych oraz zjawisk opisanych liniowymi równaniami różniczkowymi. Od lat siedemdziesiątych metodę elementów skończonych zaczęto stopniowo stosować do rozwiązywania problemów nieliniowych, ale dalej dla obiektów o stosunkowo prostych geometriach, modelowanych jako jedno– lub dwuwymiarowe. Gwałtowny rozwój techniki komputerowej w latach osiemdziesiątych, związany z coraz większą mocą obliczeniową komputerów oraz możliwością operowania i przechowywania bardzo dużych zbiorów informacji, umożliwił zastosowanie metody elementów skończonych do obliczeń problemów nieliniowych dla obiektów o dowolnie złożonych geometriach, szczególnie 3D. Bardzo duży wkład w rozwój i popularyzację metody elementów skończonych wniósł profesor Zienkiewicz z Uniwersytetu Walijskiego w Swansea. Jego książka pt. „Metoda elementów skończonych” została przetłumaczona na język polski w 1972 r.

Rozwiązanie problemu za pomocą metody elementów skończonych przebiega w kilku następujących kolejno etapach:
1. Analizowany obszar zostaje podzielony na pewną skończoną liczbę geometrycznie prostych elementów, tzw. elementów skończonych.
2. Zakłada się, że te elementy połączone są ze sobą w skończonej liczbie punktów znajdujących się na obwodach – najczęściej są to punkty narożne. Noszą one nazwę węzłów (w Calculix mamy możliwość stosowania elementów o licznie węzłów dochodzącej do 6 i więcej). Poszukiwane wartości wielkości fizycznych stanowią podstawowy układ niewiadomych.
3. Następnie obiera się pewne funkcje jednoznacznie określające rozkład analizowanej wielkości fizycznej wewnątrz elementów skończonych, w zależności od wartości tych wielkości fizycznych w węzłach. Funkcje te noszą nazwę funkcji węzłowych lub funkcji kształtu.
4. Równania różniczkowe opisujące badane zjawisko przekształcone zostają (poprzez zastosowanie tzw. funkcji wagowych) w równania metody elementów skończonych. Są to równania algebraiczne.
5. Na podstawie równań metody elementów skończonych przeprowadza się asemblację układu równań, tzn. oblicza wartości współczynników stojących przy niewiadomych oraz odpowiadające im wartości prawych stron. Jeżeli rozwiązywane zadanie jest niestacjonarne, to w obliczaniu wartości prawych stron wykorzystuje się dodatkowo warunki początkowe. Liczba równań
w układzie jest równa liczbie węzłów przemnożonych przez liczbę stopni swobody węzłów, tzn. liczbę niewiadomych występujących w pojedynczym węźle.
6. Do tak utworzonego układu równań wprowadza się warunki brzegowe. Wprowadzenie tych warunków następuje poprzez wykonanie odpowiednich modyfikacji macierzy współczynników układu równań oraz wektora prawych stron.
7. Rozwiązuje się układ równań otrzymując wartości poszukiwanych wielkości fizycznych w węzłach.
8. W zależności od typu rozwiązywanego problemu lub potrzeb, oblicza się dodatkowe wielkości.
9. Jeżeli zadanie jest niestacjonarne, to czynności opisane w pkt. 5, 6, 7 i 8 powtarza się aż do momentu spełnienia warunku zakończenia obliczeń. Może to być np. określona wartość wielkości fizycznej w którymś z węzłów, czas przebiegu zjawiska lub jakiś inny parametr.

Proste? Bynajmniej. Dlatego właśnie postanowiono zaprząc do pomocy... komputery.

Systemy CAE
Programy komputerowe, w których stosowana jest metoda elementów skończonych, składają się z trzech zasadniczych części:
• preprocesora, w którym budowane jest zadanie do rozwiązania,
• procesora, czyli części obliczeniowej,
• postprocesora, służącego do graficznej prezentacji uzyskanych wyników.

Graficzne zobrazowanie wykorzystuje m.in. skalę barw do odzwierciedlenia warunków zachodzących w badanym modelu: błękit i zieleń wskazują obszary bezpieczne, czerwień – obszary zagrożone w wyniku oddziaływania określonych sił. Stąd tytułowa „gra w kolory”...

Dla użytkowników tych programów najbardziej pracochłonnym i czasochłonnym etapem rozwiązywania zadania jest podział na elementy skończone w preprocesorze. Należy tutaj nadmienić, że niewłaściwy podział na elementy skończone powoduje uzyskanie błędnych wyników. Wtedy może okazać się, że wspomniana zieleń lub błękit, widoczne podczas komputerowej wizualizacji symulacji, tak naprawdę zamaskują przed nami fakt, iż w tym miejscu nasza konstrukcja najprawdopodobniej się... rozpadnie. 

FEA i MES (ang. FEM)
Podejście FEA (Finite Element Analysis – analiza elementów skończonych) bazuje na zasadach dyskretnych – tworzeniu macierzy sztywności dla pojedynczego elementu, agregacji elementowych macierzy sztywności w pojedynczy układ algebraicznych równań liniowych. FEA unika analizy matematycznej i jest równoważne szczególnym przypadkom metody elementów skończonych (Finite Element Method).

Analiza elementowa jest do dziś stosowana w wielu obszarach mechaniki konstrukcji, chociaż obecnie ustąpiła miejsca w powszechnym użyciu bardziej elastycznej i rygorystycznej matematycznie metodzie elementów skończonych.

Oprogramowanie FEA pozwala na przeprowadzanie wirtualnych testów, na podstawie których inżynierowie odpowiedzialni za projektowanie elementów większych instalacji mogą przewidzieć, w jaki sposób zachowają się np. zbiorniki ciśnieniowe, instalacje hydrauliczne i pneumatyczne, podnośniki, czy też rotory – w określonych warunkach środowiskowych, po zainstalowaniu ich na platformach wiertniczych, w elektrowniach wiatrowych itp. Tyle tytułem wprowadzenia.

CalculiX
Program ten, będący (podobnie jak opisywany na naszych łamach BRL-CAD) przedstawicielem systemów z grupy Open Source, liczy sobie ponad 10 lat. Powstał bowiem w 1998 roku i od tamtej pory jest systematycznie udoskonalany.

Został opracowany przez grupę entuzjastów z MTU Munich i firmy Aero Engine, którzy wykorzystali swój wolny czas do stworzenia odpowiedniego kodu, bazującego zresztą na rozwiązaniach zbliżonych do kodu wykorzystanego w systemach ABAQUS. Jego autorzy: Guido Dhondt i Klaus Wittig zastrzegają, iż liczą na to, że ten dostępny nieodpłatnie program okaże się przydatny
i użyteczny, ale...ze swej strony nie udzielają żadnych gwarancji. Cóż, wszystko zgodne z zasadami GNU General Public License. Z drugiej strony wiele firm (także polskich) z powodzeniem wykorzystuje go do swoich zastosowań. Warto nadmienić, że dostępna jest także wersja komercyjna programu w bardzo atrakcyjnej, wręcz śmiesznej cenie, której twórcy w zasadzie gwarantują poprawne działanie systemu, ale o tym za chwilę (...)

Pełny artykuł wraz z ilustracjami w numerze (w postaci plik pdf) do pobrania z Archiwum

Tutaj można pobrać wersje instalacyjne CalculiX dla Windows i dla Linux

Blog monitorowany przez: